Hockey Stick Identity Brilliant Math & Science Wiki

MathType on Twitter "This identity is known as the Hockeystick
Application This identity is used in problem 660E - Different Subsets For All Tuples. Leave a comment if you know other problems for it. In practice Naturally, if we want to calculate the binomial, we can for example use the formula $$$ \displaystyle \binom {n} {k} = \frac {n!} {k! (n-k)!} $$$ and do the division using modulo-inverse.
[Solved] Another Hockey Stick Identity 9to5Science
Another Hockey Stick Identity Asked 7 years, 7 months ago Modified 7 years, 7 months ago Viewed 1k times 4 I know this question has been asked before and has been answered here and here. I have a slightly different formulation of the Hockey Stick Identity and would like some help with a combinatorial argument to prove it.

Hockey Stick in Pascal’s Triangle Combinatorics Math Olympiad
In combinatorial mathematics, the hockey-stick identity, Christmas stocking identity, boomerang identity, Fermat's identity or Chu's Theorem, states that if are integers, then. Pascal's triangle, rows 0 through 7. The hockey stick identity confirms, for example: for n =6, r =2: 1+3+6+10+15=35. The name stems from the graphical representation of.
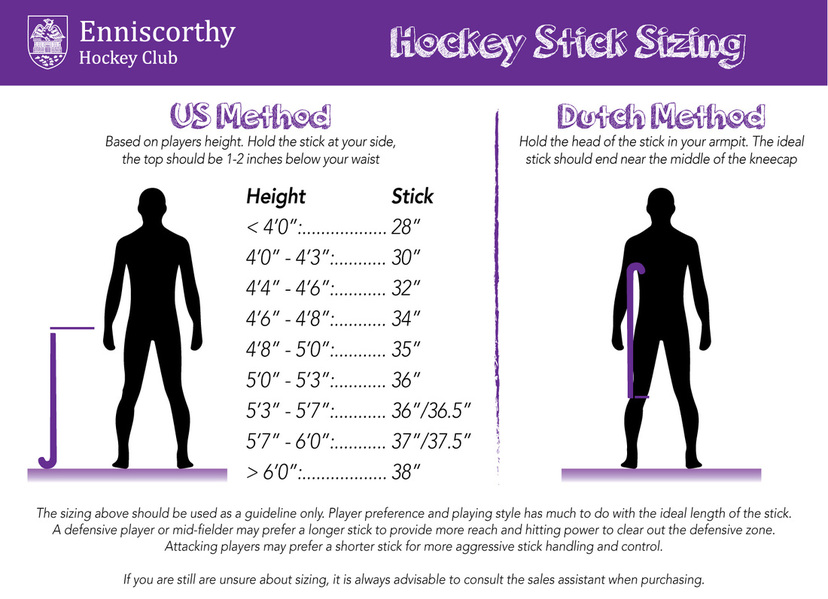
Selecting a Hockey Stick Enniscorthy Hockey Club
Math texts, online classes, and more for students in grades 5-12. Engaging math books and online learning for students ages 6-13. Small live classes for advanced math and language arts learners in grades 2-12. math training & tools Alcumus Videos For the Win!

Craft Supplies & Tools Visual Arts Hockey svg file cricut silhouette
1. Prove the hockeystick identity X r n = n + r + 1 + k k=0 k r when n; r 0 by using a combinatorial argument. (You want to choose r objects. For each k: choose the rst r k in a row, skip one, then how many choices do you have for the remaining objects?)

FileHockey stick.svg Wikimedia Commons
1 Properties 1.1 Binomial coefficients 1.2 Sum of previous values 1.3 Fibonacci numbers 1.4 Hockey-Stick Identity 1.5 Number Parity 1.5.1 Generalization 1.6 Patterns and Properties of the Pascal's Triangle 1.6.1 Rows 1.7 Diagonals 2 See Also Properties Binomial coefficients These are the first nine rows of Pascal's Triangle.

Hockey Stick Identity Brilliant Math & Science Wiki
0:00 / 10:42 Art of Problem Solving: Hockey Stick Identity Part 1 Art of Problem Solving 71.2K subscribers Subscribe 19K views 11 years ago Art of Problem Solving's Richard Rusczyk.

Art of Problem Solving Hockey Stick Identity Part 2 YouTube
The hockey stick identity in combinatorics tells us that if we take the sum of the entries of a diagonal in Pascal's triangle, then the answer will be anothe.

Kookaburra Composite Hockey Stick Identity SKU KKBR_CIDTT www
Hockey-stick identity - Wikipedia Hockey-stick identity Pascal's triangle, rows 0 through 7. The hockey stick identity confirms, for example: for n =6, r =2: 1+3+6+10+15=35.

Hockey Stick Size Guide With Sizing Chart Net World Sports
The hockey stick identity is an identity regarding sums of binomial coefficients. For whole numbers n n and r\ (n \ge r), r (n ≥ r), \sum_ {k=r}^ {n}\binom {k} {r} = \binom {n+1} {r+1}. \ _\square k=r∑n (rk) = (r+ 1n+1). The hockey stick identity gets its name by how it is represented in Pascal's triangle.

Art of Problem Solving Hockey Stick Identity Part 1 YouTube
Let's discuss the Hockey Stick Identity from Combinatorics in Pascal's Triangle.https://www.cheenta.com/matholympiad/Visit https://www.cheenta.com/ for Advan.
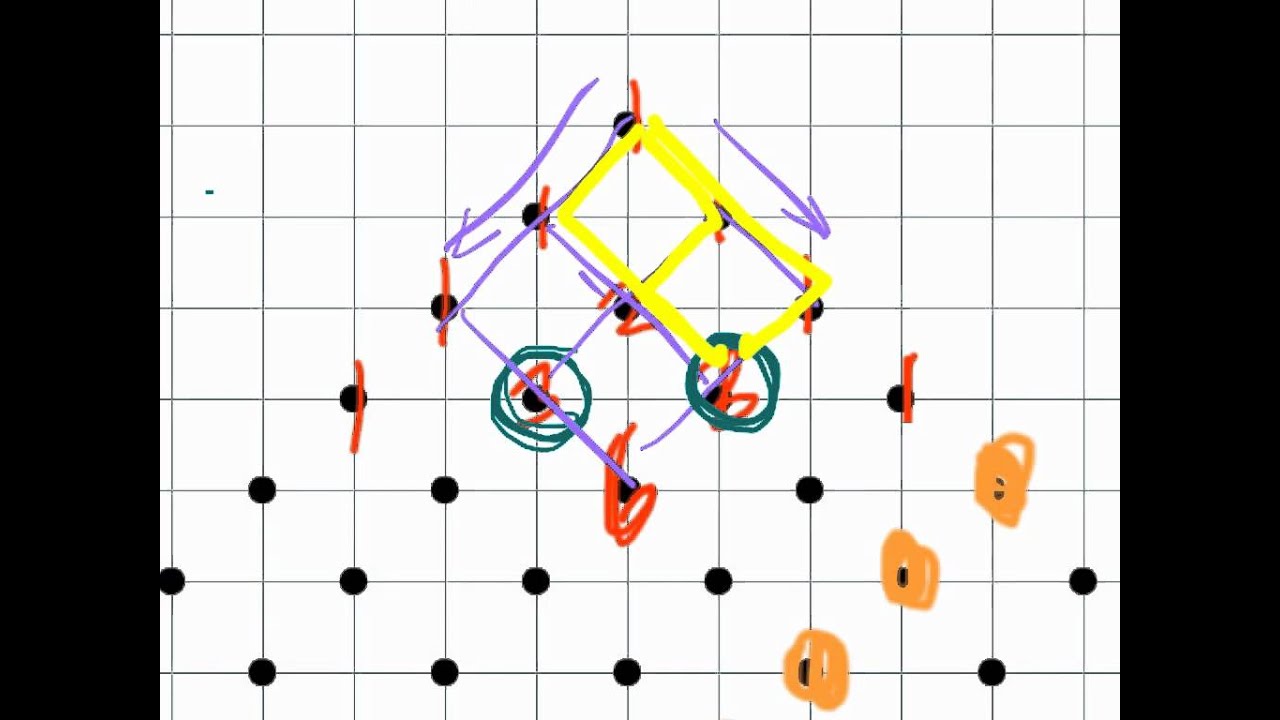
Hockey stick identity, argued via path counting YouTube
EDIT 01 : This identity is known as the hockey-stick identity because, on Pascal's triangle, when the addends represented in the summation and the sum itself are highlighted, a hockey-stick shape is revealed. combinatorics combinations binomial-coefficients faq Share Cite Follow edited Feb 7, 2023 at 6:25 Apass.Jack 13.3k 1 20 33

Kookaburra Composite Hockey Stick Identity SKU KKBR_CIDTT www
We look at summation notation, and we are trying to solve 13.3. We think about forming a committee of 4 people, assuming that the members arrive not all at o.

Hockey Stick Identity Brilliant Math & Science Wiki
example 5 Use combinatorial reasoning to establish the Hockey Stick Identity: The right hand side counts the number of ways to form a committee of people from a group of people. To establish this identity we will double count this by assigning each of the people a unique integer from to and then partitioning the committees according to the.

What Does Flex on a Hockey Stick Mean KasonhasHorn
Hockey stick. For . This identity is known as the hockey-stick identity because, on Pascal's triangle, when the addends represented in the summation and the sum itself is highlighted, a hockey-stick shape is revealed. Proof. Inductive Proof. This identity can be proven by induction on . Base Case Let . . Inductive Step Suppose, for some , . Then .

Hockey Stick Identity Brilliant Math & Science Wiki
Combinatorial identity Contents 1 Pascal's Identity 1.1 Proof 1.2 Alternate Proofs 2 Vandermonde's Identity 2.1 Video Proof 2.2 Combinatorial Proof 2.3 Algebraic proof 3 Hockey-Stick Identity 3.1 Proof 4 Another Identity 4.1 Hat Proof 4.2 Proof 2 5 Even Odd Identity 6 Examples 7 See also Pascal's Identity Pascal's Identity states that