How to Find the Derivative of a^x from First Principles YouTube

Differentiation from 1st Principles Calculus by ExamSolutions YouTube

STEP 1: Identify the function f (x) and substitute this into the first principles formula e.g. Show, from first principles, that the derivative of 3x2 is 6x so STEP 2: Expand f (x+h) in the numerator STEP 3: Simplify the numerator, factorise and cancel h with the denominator STEP 4: Evaluate the remaining expression as h tends to zero

Differentiating from first principles YouTube

Calculus Differentiating Trigonometric Functions Differentiating sin (x) from First Principles Key Questions How do you differentiate f (x) = sin(x) from first principles? Answer: d dx sinx = cosx Explanation: By definition of the derivative: f '(x) = lim h→0 f (x + h) − f (x) h So with f (x) = sinx we have; f '(x) = lim h→0 sin(x +h) − sinx h

Differentiation 1 eg. 2.2 First principles YouTube

Definition The derivative of a function f(x) f ( x) is denoted by f′(x) f ′ ( x) and is defined as f′(x) = limh→0 f(x + h) − f(x) h, h≠ 0. f ′ ( x) = lim h → 0 f ( x + h) − f ( x) h, h ≠ 0. Using this definition is called differentiating from first principles. The result f′ (x) f ′ ( x), is called the derivative of f(x) f ( x).

[Solved] Differentation from first principles apparent 9to5Science

1 DN1.1: DIFFERENTIATION FROM FIRST PRINCIPLES The process of finding the derivative function using the definition '( x ) = ( x + h f x lim ( ) , h ≠ 0 → 0 is called differentiating from first principles. Examples 1. Differentiate x2 from first principles. f + ′ ( ) x = lim h → 0 = lim h→ 0 = lim h→ 0 = lim h→ 0 = lim h→ 0 = lim h→ 0

Differentiation from First Principles a simple explanation of how it works YouTube

In this video we focus on the first Principle of Differentiation, a component of calculus that explains how to determine the derivatives of functions.#learnt.

Derivative of x^2 from First Principles YouTube

Derivative by first principle refers to using algebra to find a general expression for the slope of a curve. It is also known as the delta method. The derivative is a measure of the instantaneous rate of change, which is equal to f' (x) = \lim_ {h \rightarrow 0 } \frac { f (x+h) - f (x) } { h } . f ′(x) = h→0lim hf (x+h)−f (x).

SPM (Add Maths) Differentiation by First Principle Rule YouTube

The First Principles technique is something of a brute-force method for calculating a derivative - the technique explains how the idea of differentiation first came to being. A Level AQA Edexcel OCR Finding Derivatives from First Principles To differentiate from first principles, use the formula

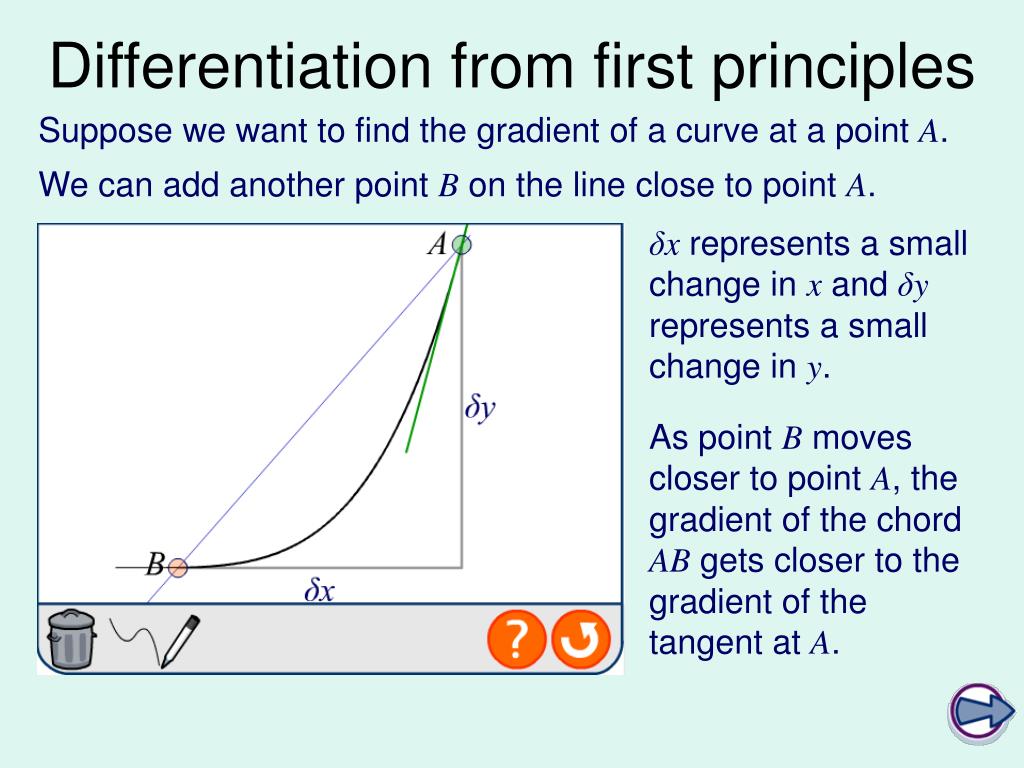
PPT C1 Differentiation from First Principles PowerPoint Presentation ID1806096

The differentiation by first principles formula is f' (x)=limh→0[f (x+h)- (fx)]/h. For any function f (x), find f (x+h) by replacing x with x+h and substitute f (x+h) and f (x) into the formula. Simplify the numerator and divide all terms by h. Finally evaluate the limh→0 by substituting h = 0. The result is the gradient function of f (x).

How to Differentiate by First Principles

Using first principles, the derivative of the exponential function c^x can be simplified, however, determining the actual limit is best done by using a computer.

Differentiation by First Principle Examples YouTube

Differentiation From First Principles This section looks at calculus and differentiation from first principles. Differentiating a linear function A straight line has a constant gradient, or in other words, the rate of change of y with respect to x is a constant. Example Consider the straight line y = 3x + 2 shown below

More examples of differentiating from first principles. YouTube

First Principle of Differentiation: Derivative as a Rate Measurer, Geometrical Interpretation of Derivative at a Point A derivative is the first of the two main tools of calculus (the second being the integral). It is the instantaneous rate of change of a function at a point in its domain.

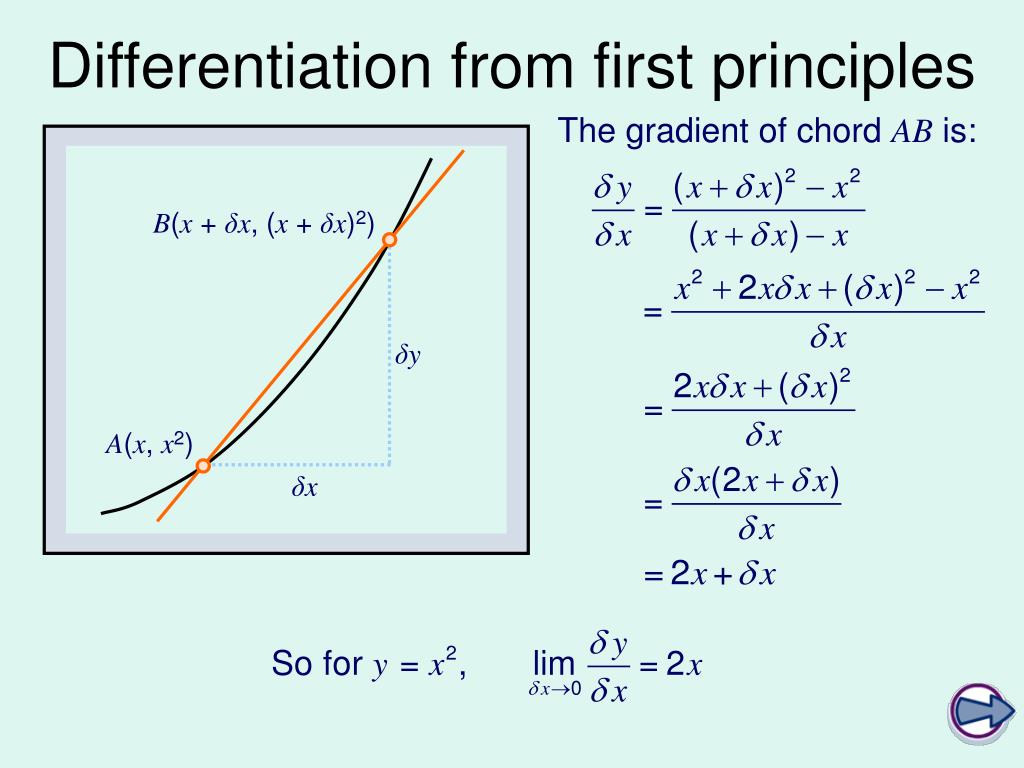
PPT C1 Differentiation from First Principles PowerPoint Presentation ID1806096

The process of determining the derivative of a given function. This method is called differentiation from first principles or using the definition. Worked example 7: Differentiation from first principles Calculate the derivative of \ (g\left (x\right)=2x-3\) from first principles.

Differentiation from first principles Teaching Resources

A Level Maths revision tutorial video.For the full list of videos and more revision resources visit www.mathsgenie.co.uk.

Differentiation by First Principle All Formulae of Differentiation YouTube

Project Team:Daphne Li, Bon Tsang, Cindy Chan, Florence Chan, Leo Fung, Jim Cho, June Hui, Vivian Tsang, Cherry Chin, Esther Ma. Cost Consultant: Northcroft HK Ltd. Client:Architectural Services.

9 Differentiation from first principles YouTube

We now have a formula that we can use to differentiate a function by first principles. Let's try it out with an easy example; f (x) = x 2. In this example, I have used the standard notation for differentiation; for the equation y = x 2, we write the derivative as dy/dx or, in this case (using the right hand side of the equation), dx 2 /dx.

PPT C1 Differentiation from First Principles PowerPoint Presentation ID1806096

STEP 1: Identify the function f (x) and substitute this into the first principles formula. e.g. Show, from first principles, that the derivative of 3x2 is 6x. so. STEP 2: Expand f (x+h) in the numerator. STEP 3: Simplify the numerator, factorise and cancel h with the denominator. STEP 4: Evaluate the remaining expression as h tends to zero.